Hình bình hành là một hình học quen thuộc , có nhiều ứng dụng trong cuộc sống. Trong bài viết này chúng tôi sẽ chia sẻ công thức Diện tích hình bình hành và bài tập áp dụng liên quan.
MENU
Khái niệm và tính chất của hình bình hành
Khái niệm
Hình bình hành trong hình học Euclid chính là một hình tứ giác được tạo thành khi hai cặp đường thẳng song song. Đây là 1 dạng đặc biệt của hình thang gồm 4 góc và có những tính chất giống với hình thang và hình chữ nhật.
Hình bình hành có nhiều ứng dụng trong cuộc sống. Như trong xây dựng, thiết kế, và khoa học máy tính. Đây cũng là một trong những loại hình cơ bản được học trong môn hình học và toán học.
Một số ví dụ về hình bình hành gồm: hình bình chữ nhật (là một loại hình bình hành đặc biệt với 4 cạnh đều vuông góc với nhau), hình thoi (là một loại hình bình hành có các cạnh bằng nhau và các góc đối diện có cùng độ lớn), và hình bình hành đều (là một loại hình bình hành có cả 4 cạnh bằng nhau và các góc đối diện có cùng số đo).

Tính chất hình bình hành
Tính chất của hình bình hành
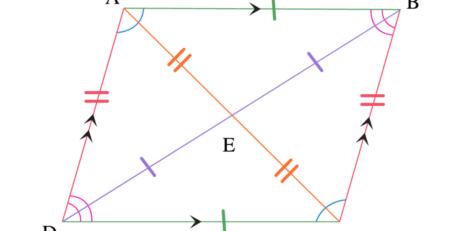
Hình bình hành sở hữu một số tính chất đáng chú ý như sau:
Hai đường chéo của hình bình hành cắt nhau tại trung điểm mỗi đường và chia đôi hình bình hành thành 2 tam giác đồng dạng.
Các cặp đối song song và bằng nhau
Các góc đối bằng nhau
>> Xem thêm: Giá thuê xe ô tô tự lái tại đà nẵng
Công thức tính diện tích hình bình hành
Công thức Diện tích hình bình hành được phát biểu như sau:
Diện tích hình của bình hành sẽ bằng độ dài cạnh đáy nhân với độ dài chiều cao.
Gọi B là độ dài cạnh đáy, và H là độ dài chiều cao và S là diện tích, ta có:
S = B x H

Công thức tính diện tích của hình bình hành
Ngoài ra, diện tích của hình bình hành cũng được tính bằng tích độ dài 2 cạnh kề nhân với sin góc hợp bởi 2 cạnh đó.
Gọi A và B lần lượt là độ dài 2 cạnh và ⍺ là góc hợp bởi 2 cạnh trên. Ta có Diện tích của hình bình hành bằng:
S= A x B x sin ⍺
Chu vi hình bình hành
Chu vi hình bình hành được tính bằng tổng độ dài các đường bao quanh hình, hay chính là đường bao quanh toàn bộ diện tích, nó bằng 2 lần tổng một cặp cạnh kề nhau bất kỳ.
Chu vi hình bình hành chính là tổng độ dài của 4 cạnh. Công thức cụ thể như sau:
C = 2 x (a+b)
Trong đó:
C là chu vi của hình bình hành.
a và b là độ dài 2 cạnh kề nhau trong hình bình hành.
Tham khảo: Phố cổ hội an thuộc thành phố nào
Các dạng bài tập áp dụng Diện tích hình bình hành
Dạng 1: Tính diện tích khi đã biết độ dài đáy và chiều cao
Phương pháp: Với dạng bài tập này, bạn chỉ cần áp dụng đúng công thức tính diện tích S = B x H để ra kết quả.
Ví dụ: Tính diện tích của hình bình hành có độ dài đáy bằng 8 cm và chiều cao bằng 5 cm.

Bài tập áp dụng tính diện tích của hình bình hành
Giải:
Áp dụng công thức ta có: S = B x H
S = 8 x 5 = 40 cm2
Vậy diện tích của hình bình hành là 40 cm².
Dạng 2: Tính độ dài cạnh đáy cho biết diện tích và chiều cao hình bình hành
Phương pháp: Từ công thức chuẩn S = B x H, ta suy ra được công thức tính độ dài cạnh đáy như sau: B = S : H.
Ví dụ tính độ dài cạnh đáy hình bình hành có diện tích bằng 100 cm² và chiều cao bằng 10 cm.
Giải:
Từ công thức S = B x H=> B = S : H.
Thay số liệu vào ta có:
B = S : H = 100 : 10 = 10 cm
Vậy độ dài đáy của hình bình hành trên là 10 cm.
Dạng 3: Tính chiều cao khi biết diện tích và độ dài của đáy hình bình hành
Phương pháp: Từ công thức S = B x H, suy ra công thức tính chiều cao là H = S : B
Ví dụ: Tính chiều cao của hình bình hành có diện tích bằng 80cm² và cạnh đáy bằng 5 cm.
Giải:
Ta có độ dài chiều cao: H = S : B= 80 : 5 = 16
Vậy độ dài chiều cao hình bình hành là 16cm
Dạng 4: Tính diện tích hình của bình hành khi biết được diện tích hình chữ nhật và diện tích hình tam giác cấu tạo nên nó.
Phương pháp: Đầu tiên bạn cần xem xét diện tích hai hình đã cùng đơn vị hay chưa. Nếu chưa, hãy quy đổi cùng đơn vị đo diện tích. Tiếp đó sử dụng phép tính tổng để tính diện tích của hình bình hành.
Ví dụ: Tính diện tích của hình bình hành cho biết diện tích hình chữ nhật và tam giác cấu tạo nên nó như sau:
Diện tích của hình chữ nhật S1 = 10 cm2
Diện tích hình tam giác S2 = 500 mm2
Giải:
Đổi diện tích hình tam giác S2 = 500 mm2 = 5 cm2
Diện tích của hình bình hành: S = S1 + 2 x S2 = 10 + 2 x 5 = 10 + 10 = 20 cm2
Trên đây là những thông tin chi tiết và cách giải bài tập liên quan đến diện tích của hình bình hành. Hy vọng qua thông tin trên, các em đã biết áp dụng và giải bài tập dễ dàng.